散乱の量子論

最終更新日：2023.4.26

これまで、散乱は現象論として扱われることが多かったのですが、ここでは量子論を使って散乱関数を誘導します。量子力学、量子化学を習った人には少し馴染みがあるかもしれません。量子論に基づいて散乱現象を記述すると、高エネルギー物理などの分野との繋がりも見えてきます。
Scattering has often been treated as a phenomenology, but here we use quantum theory to induce scattering functions. This may be a little familiar to those who have studied quantum mechanics and quantum chemistry. Describing scattering phenomena based on quantum theory also reveals connections to fields such as high-energy physics.

---

まずは波動関数から微分方程式の誘導まで
First, from wave functions to differential equation induction.

---

次は、グリーン関数を用いて微分方程式を解きます。練習問題Q1, Q2もあるので是非、挑戦してみてください。
Next, we will solve differential equations using the Green's function. There are also exercises Q1 and Q2, so please give them a try.

---

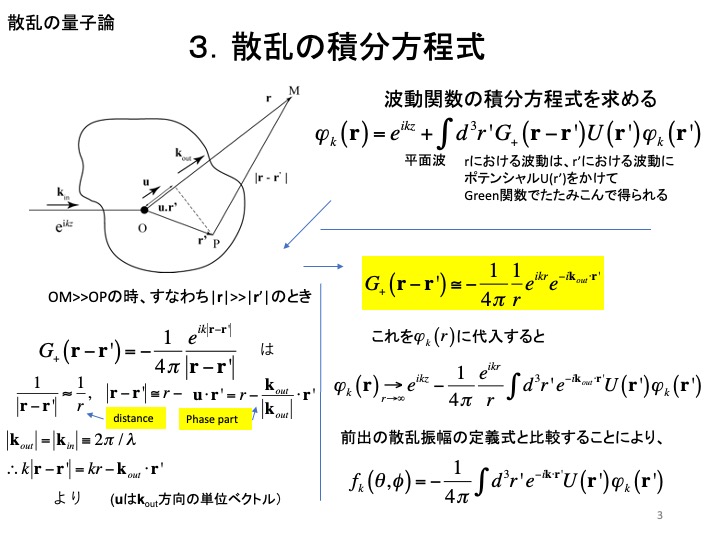
波動関数の積分表示をします。
Display the integral of the wave function.