ベクトル場の積分:ファイマン(Feynman)先生の電磁気学 Integration of vector fields: Prof. Feynman's Electromagnetics
最終更新日:2024.3.26
電磁気学ではベクトル場の積分に関する公式や定理がたくさんでてきます。とくにマクスウェルの電磁気学となると、これらのオンパレードとなるので、学ぶ前から電磁気学を嫌いになった人も多いとおもいます。私もその1人です。でも、マクスウェル方程式には物理学の叡智が込められているので、そのさわりとなるベクトル場の積分を少しだけでもかじっておきましょう。
In electromagnetism, there are many formulas and theorems related to integrals of vector fields. Especially when it comes to Maxwell's electromagnetism, there are many people who dislike electromagnetism even before they learn it because of the parade of these formulas and theorems. I was one of them. However, Maxwell's equations contain the wisdom of physics, so it is important to learn at least a little bit about vector field integration, which is a rough introduction to the subject.
ベクトル解析:ベクトル場の積分 ector analysis: Integration of vector fields

ベクトル場の積分公式 integral formulas for vector fields
ベクトル場の積分公式をリストしました。どれも有名かつ有用な公式です。次のページからはそれらの意味を一緒に考えてみましょう。
I have listed the integral formulas for vector fields. They are all well-known and useful formulas. Let's consider their meanings together from the next page.

スカラー場の微分の線積分 Line integral of the derivative of a scalar field
スカラー場の微分の線積分です。力と仕事(ポテンシャル)の関係を思い浮かべればいいでしょうか。
This is the line integral of the derivative of a scalar field. Can you think of the relationship between force and work (potential)?


面積分と体積積分 Area and volume integrals
面積分と体積積分を結びつける式です。電磁気学ではガウスの定理として有名で、場の保存を表す式です。たとえていうと、収穫ロスを見積もるのに、漁網の隙間から逃げていく魚を数てもいいし、網の中の魚の総重量の変化を量ってもいい、ということでしょうか。
It is an equation that connects area and volume integrals. In electromagnetism, it is well known as Gauss's theorem and is an expression for conservation of field. To use an analogy, you can estimate the harvest loss by counting the number of fish escaping through the gaps in the fishing net or by weighing the change in the total weight of the fish in the net.

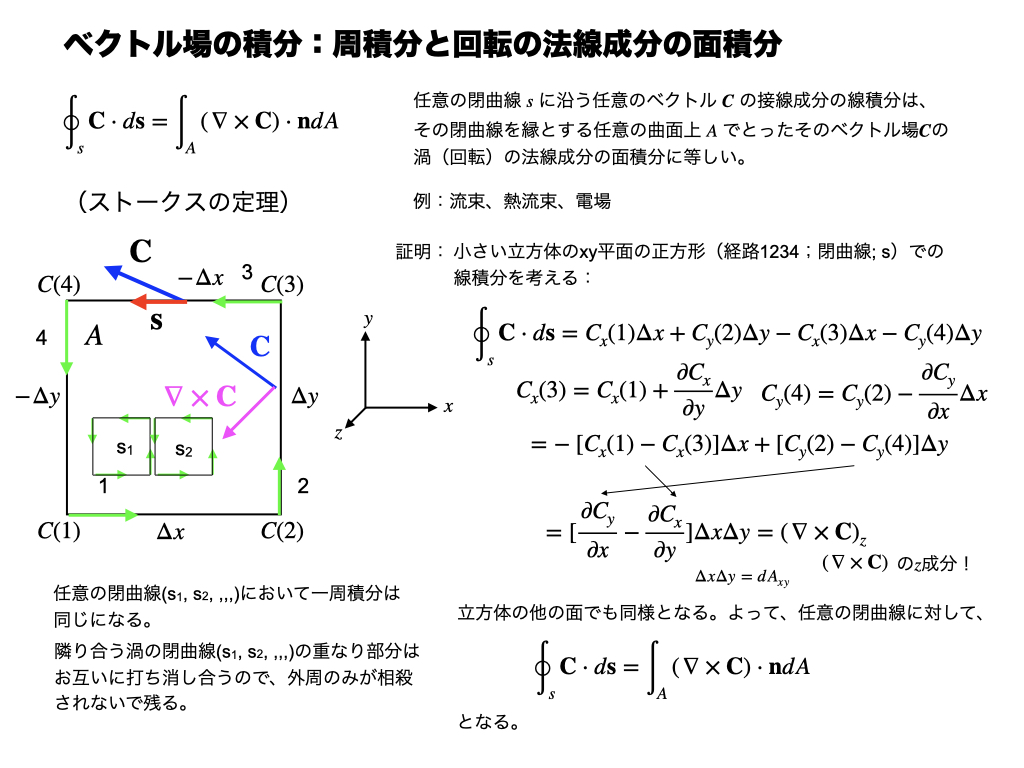
周回積分と回転の法線成分の面積分 circulant integral and area integral of the normal component of the rotation
周回積分と回転の法線成分の面積分を結びつける式です。電磁気学ではストークスの定理として有名で、渦をあらわす式です。何にたとえたらいいか、みなさんもかんがえてみてください。
It is an equation that connects the circumferential integral with the area component of the normal component of the rotation. In electromagnetism, it is well known as Stokes' theorem and is an expression for vortices.