3次元フーリエ変換(3D Fourier Transform)

最終更新日：2023.5.1

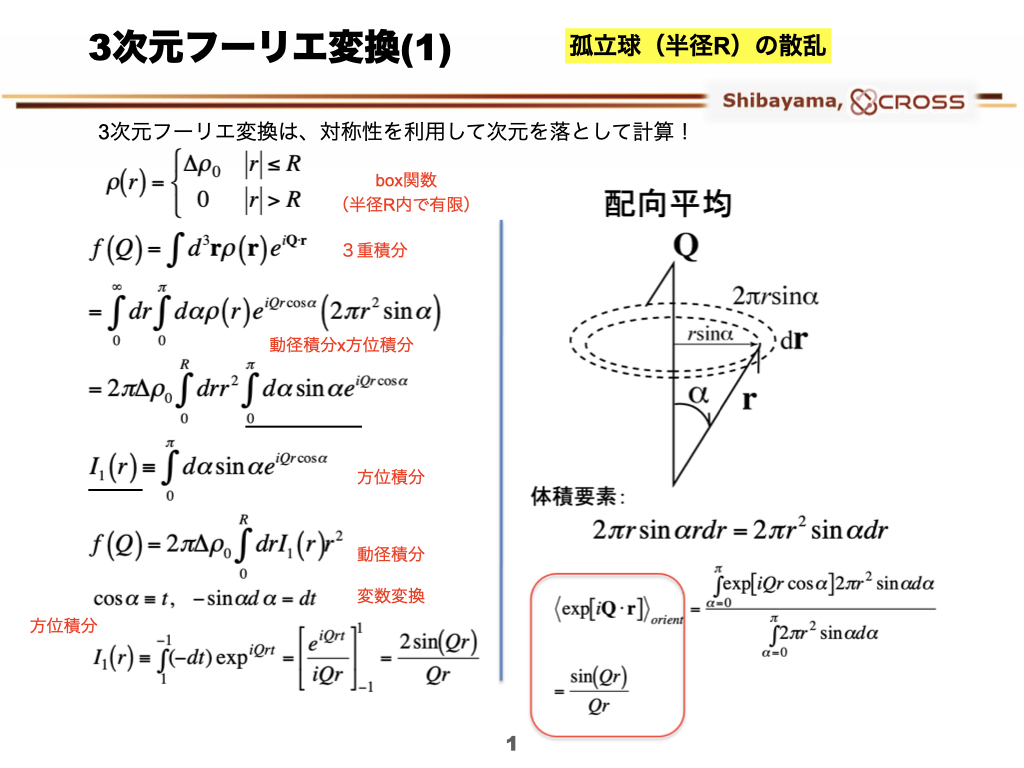
3次元フーリエ変換の例として球状粒子の3次元フーリエ変換を行い、球の散乱関数を求めます。フーリエ変換の次元が高くなると、計算がどんどん難しくなるのですが、球のように対称性がある系の場合、対称性を利用して次元を落として計算できます。この場合、3次元積分が方位と動径の２重積分になります。また、球の散乱関数は、球の体積の2乗、および球内外の散乱長密度差の2乗に比例することに注意しましょう。
As an example of a 3-D Fourier transform, the 3-D Fourier transform of a spherical particle is used to obtain the scattering function of the sphere. As the dimension of the Fourier transform increases, the calculation becomes more and more difficult. However, for a system with symmetry, such as a sphere, the symmetry can be used to reduce the dimension of the calculation. In this case, the three-dimensional integration becomes a double integral of the azimuth and the radius. Also note that the scattering function of a sphere is proportional to the square of the volume of the sphere and the square of the difference in scattering length density between the inside and outside of the sphere.

---

---

---

---