単一指数関数と広幅分布関数

2011.3.29; 最終更新日：2014.9.18

プルンプルンとした弾力のあるゲルとぶよぶよのゲルでは何がちがうのでしょうか。

---

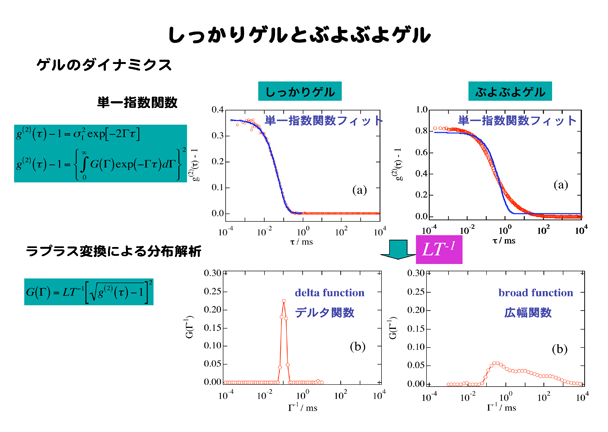
ふつう高分子ゲルは自分で自分の形を保つことのできる「しっかりゲル」ですが、架橋剤を減らしてゲルをつくるとやがて、ゲルかゾルかわからないような「ぶよぶよゲル」ができます。これら２つのゲルのダイナミクスが全く違い、「しっかりゲル」の時間相関関数は単一指数関数でフィットできるある特定の緩和時間(tau)をもつダイナミクスとなります。すなわち、ゲル中の高分子鎖はみんな一緒に同じ調子で動いています。これに対し、架橋剤濃度を低くしてつくった「ぶよぶよゲル」は速いモードや遅いモードが混在する幅広いダイナミクス分布を持ちます。あたかも、ちいさなはちどりから大鷲にわたるさまざまなサイズのとりが一斉に羽ばたいたときのようにひろい分布があります。こうした「はばたきの分布」は相関関数を逆ラプラス変換(LT^-1)して求まる分布関数G(gamma^-1)にて一目瞭然です。「しっかりゲル」では単一モードであるデルタ関数的な分布となり、「ぶよぶよゲル」では幅の広い分布がでてきます。
M. Shibayama, Macromolecules, 1998, 31, 5316.