フラクタル次元

最終更新日：2014.9.18

フラクタル、フラクタル次元ってきいたこと、ありますか？修士１年の学生さん２人が、身近な材料を使ってフラクタルの実験をしてくれました。2004年のことでした。(2004.4.15)
この実験のアイデアは、1983年に筆者がアメリカ留学中に聴講した講演会に基づいています。臨界現象研究の権威であるボストン大学Eugen H. Stanley教授がデモンストレーションで、様々な大きさの紙を丸めて、直径と重さと関係をプロットすると、フラクタル次元が得られるという実験結果を紹介しました。

「フラクタル」とは何でしょう。フラクタルとは、部分と全体の構造が同じ形をしているもののことをいいます。難しい言葉でいうと「自己相似性」の物体。フラクタルの例には、コッホ曲線やシェルビンスキーのカーペットというものがあります。また、自然の中には多くのフラクタル構造が潜んでいて、山の形、リアス式の海岸線の形、河川の中流付近の形、雲の形、樹木、葉などにもみられます。

それでは、身近な材料で、フラクタル次元を実感してみましょう。実験は、球の直径に対する体積と質量の関係を調べることで、フラクタル次元を調べるというものです。
球の体積VはR3に比例するから、V~ R^3でであることは知っていますね。でも、球の質量Mは密度が一様でなければどうでしょうか？　
まず、DをV~ R^D と定義します。
つぎに、実験の準備をしましょう。
エナメル線（太さ　0.1mm　長さ２０ｍぐらい）、市販のアルミ箔（１ｍ）、ノギス、メジャー、化学天秤を用意します。エナメル線、アルミ箔をそれぞれ加工します。

加工といっても、写真にあるように、どちらも手で「丸める」だけです。しっかり丸めてから、それらの重さを量ると、以下のような関係が得られました。エナメル線については、エナメル線の長さと、その重さの間に、
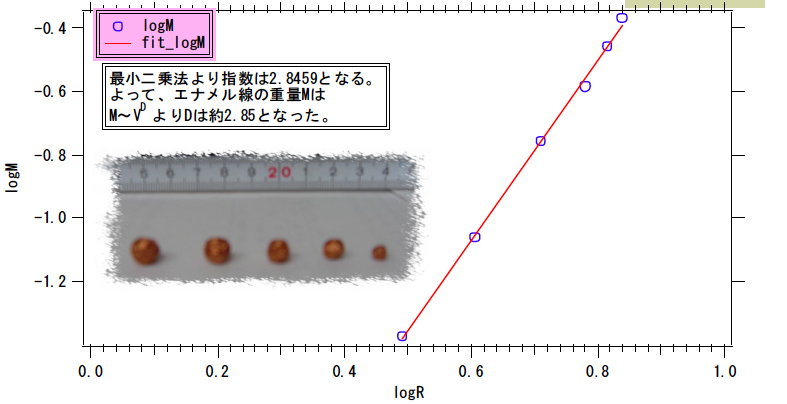
という関係が見いだされました。これから、フラクタル次元Dは2.85　と求まりました。一方、アルミ泊からは　　
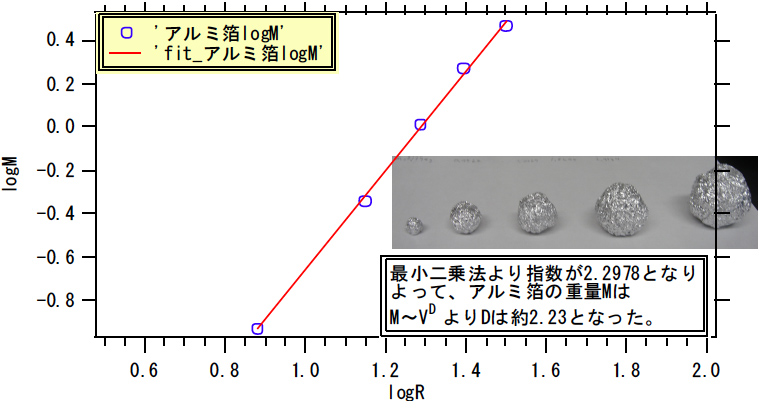
という関係が得られ、フラクタル次元Dは2.30　と求まりました（ミスプリは愛嬌）。
実験をする前には、１次元のエナメル線を丸めた方が、２次元のアルミ泊を丸めた物より、フラクタル次元は小さいと予想していたのですが、結果は逆でした。紐状のエナメル線の方が丸めやすかったのかもしれませんね。皆さんもやってみませんか。　